Cycloids

In the applet above you can see a cycloid being traced by a point on the circumference of a rolling wheel. Click on the applet to restart the animation.

Let us try to obtain the equation of this cycloid. The coordinate system we use has its origin at the top-left corner of the applet, and, as is usual on computer screens, the y-axis points down. In the usual Cartesian coordinate system that we are familiar with, the y-axis points up and the positive sense of rotation is anti-clockwise. Here, however, the positive sense of rotation is clockwise.

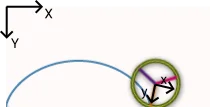
But first let us consider a static wheel rotating about its center. We place the origin at the center of the wheel. Then, the x and y coordinates of a point at a distance r from the center that starts rotating from the position $(r, 0)$ are

where $\theta$ is the angle of rotation.

In the animation above the point that traces the cycloid starts from the bottom of the wheel, $(0, r)$. For such a point the starting angle is $\pi/2$ and not $0$. The above equations then become

To obtain the equation of the cycloid we have to transform these coordinates to a frame attached to the track along which the wheel is rolling. This is the one with the origin at the top-left corner.

For a rolling wheel the center of the wheel is no longer static and is also moving. When a point on the circumference of the wheel( as seen from a reference frame attached to the wheel ) rotates through an angle $\theta$, it moves a distance $r\theta$ along the circumference. With respect to the track frame, this is the same distance that the wheel or the center of the wheel has moved ahead. Thus, in the track frame, the coordinates of the tracing point are

Here, $(X_c, Y_c)$ are the coordinates of the center of the wheel in the track frame. $h$ is the height of the applet. This is the equation of the cycloid.

The applet is programmed in Elm. As of now, Elm is a language for front-end development and is an alternative to using frameworks such as React, Vue, or Angular. It is also an alternative to using Typescript, ReScript, and others because though these languages make things easier(compared to Javascript) by having a type system you still have to learn to use a front-end framework like React. With Elm you just have to learn Elm because in addition to the appealing syntax and programming paradigms the language provides it gives you a recipe to structure and build web applications. But the USP of Elm is this: if your Elm program compiles fine you are guaranteed that you will have no runtime errors.

Unlike Javascript, Elm supports only functional programming. Functional programming has several advantages and for the most of us that are used to imperative programming, some annoyances too. Functional programming gets its name from the use of pure functions. A pure function takes an input and produces an output, and does nothing else. Much like a function in mathematics, $z = f(x, y)$. In Javascript or C a function need not return anything(which means it returns undefined or void) and can still affect the environment by, say, changing a global variable, printing to the console, producing a beep, or drawing on a canvas. In the functional programming world these are called side-effects and are forbidden. Any change a purely functional program causes has to be through the output or return value of a function.

It will be too much to provide a full tutorial on Elm here. Please refer to the official guide or a good unofficial one. Nevertheless, I shall mention a few things that can make the following code appear less unfamiliar.

In Elm every value has a definite type that cannot be changed. You can associate a value with a name, as in x = 5 and use that name in place of that value. In an Elm program a name can be a type, a constant, or a function. In the program given below, Msg is a type, angleInc a constant, and turnsAndRadius a function. There are no variables in Elm. The x at the beginning of this paragraph is not a variable as it would be, say, in Javascript. In particular, this means that you cannot have an expression of the form x = x + 3.

The Model type below is an example of a record type. This is similar to an object in Javascript or a struct in C or Go. The Msg type is a union or custom type. This is similar to an union type or enumeration type in languages such as C but much much more powerful. The Msg type defined here has four variants, each separated from the previous by |. Each variant can be just a tag or a tag followed by another data type. This data type is the type of the data that can be associated with the variant. For example, the NextFrame variant has Float data associated with it. Pattern matching is used to distinguish between the variants as you can see in the update function.

The Result type associated with the Msg variant HolderElement is used to handle computations that may fail. This is much more robust than using null or nil or undefined for handling failure. This has two variants - an Ok variant and an Err variant. The Ok variant has associated with it the value of a successful computation and the Err variant has associated with it the error if the computation fails.

type alias Model =
    { turns : Int
    , radius : Float
    , rotn : Float
    , path : String
    }


type Msg
    = HolderElement (Result Error Element)
    | NextFrame Float
    | Restart
    | Resized

In variable or function definitions in C or Go the type of a value is specified by its side, before or after. In Elm that's not how it is. The types are specified in a separate type annotation. It is recommended but not mandatory that a constant or a function be prefixed by a type annotation. svgheight : Float is a type annotation for the constant svgheight. turnsAndRadius : Float -> ( Int, Float ) says that the turnsAndRadius function takes a Float and returns a ( Int, Float ) tuple. Notice that the parameters and return value are separated by arrows in the annotation. In the function definition, however, the parameters are separated by spaces and there is no mention of any type.

Functions in Elm support partial application. Suppose you have a function fn : Float -> Int -> String. This takes two parameters of type Float and Int and returns a String. But suppose you were to call the function with just one argument of type Float. This would be perfectly ok and it would return another function that can accept an argument of type Int and return a String.

The recipe that Elm provides to structure a web application is called The Elm Architecture. This is similar to and derived from the Model View Controller(MVC) design pattern. Here, the Controller is the Elm runtime. The state of the application is held in a type defined as Model. Every event the application responds to is handled by a variant of Msg. An update function receives these Msg variants and returns a new Model. A view function is wired to take this new Model and return new html which then updates the display. This is the essence of the Elm Architecture.

The function init is run at the start of the application. This is defined as a function that takes an empty tuple(which we are not using here anyway) and returns the initial Model as the first element of a tuple. The second element of the tuple is a command that we send to the runtime. This is represented by the Cmd Msg data type - a command that responds with a message to our application. Here, we are fetching the element with the id "app_holder". As you can see from the source, "app_holder" contains the application which is just an SVG element. The width of this element is used to determine the width of the contained SVG. A media query restricts the width to 600px or 300px when the screen width is above 640px or not. The Msg variant is HolderElement. That's what I am calling it. Now it is possible that the element you are trying to fetch isn't there. Perhaps, the id was misspelt or perhaps it wasn't included in the first place. In any case there is a possibility of an error here. This is why the data associated with HolderElement is a Result type. I have already talked about the Result type. The point is that you are forced to handle the possibility of an error.

init : () -> ( Model, Cmd Msg )
init _ =
    let
        ( turns, radius ) =
            turnsAndRadius 300
    in
    ( Model turns radius 0 ("M 0," ++ fromFloat svgheight)
    , Browser.Dom.getElement "app_holder" |> Task.attempt HolderElement
    )

I have arbitrarily set the number of full turns the wheel goes through as it rolls from the beginning to the end to be 3 for the smaller width and 4 for the larger one. This allows me to determine the radius of the wheel in each case. The Model stores the number of full turns, the radius, the angle the wheel has rotated through( in the wheel's frame of reference ), and a string that will form the d attribute of the SVG path that will be the cycloid. The path string is initialized to "M 0, 100". The height of the SVG element is 100 pixels.

As I have said, every time the model is updated the view function is run. In addition, the subscriptions function is also run. A command is a one-shot thing. A subscription is like a long-standing command. To quote from the official documentation, A subscription is a way of telling Elm, 'Hey, let me know if anything interesting happens over there!'. You can use subscriptions to listen to web socket messages, clock ticks, requestAnimationFrame messages etc. Here, we are subscribing to requestAnimationFrame and resize messages.

subscriptions : Model -> Sub Msg
subscriptions model =
    if model.rotn < toFloat model.turns * 2 * pi then
        Sub.batch [ BE.onAnimationFrameDelta NextFrame, BE.onResize (\_ _ -> Resized)   ]

    else
        BE.onResize (\_ _ -> Resized)

The Resized message in turn fires a HolderElement message which resets the model with the new width.

update msg model =
	...
    HolderElement (Ok holderElement) ->
        let
            ( turns, radius ) =
                turnsAndRadius holderElement.element.width
        in
        ( { model | turns = turns, radius = radius, rotn = 0, path = "M 0," ++ fromFloat svgheight }, Cmd.none )
    Resized ->
        ( model, Browser.Dom.getElement "app_holder" |> Task.attempt HolderElement )
    NextFrame _ ->
    let
        newRotn =
            model.rotn + angleInc

        x =
            model.radius * (newRotn - sin newRotn)

        y =
            svgheight - model.radius * (1 - cos newRotn)

        newPath =
            model.path ++ " L " ++ fromFloat x ++ "," ++ fromFloat y
    in
    ( { model | rotn = newRotn, path = newPath }, Cmd.none )

The interesting stuff happens in the handling of the NextFrame message. It is here that we use the formulas derived above to calculate a new point on the cycloid.

Once a new model has been produced by the update function, the view function is run. The view function draws an SVG containing the cycloid and the wheel.

view : Model -> Html Msg
view model =
    svg
        [ width "100%"
        , height "100%"
        , onClick Restart
        ]
        [ trace model.path
        , wheel model.radius model.rotn
        ]

Notice that the SVG element sends a Restart message that resets the application when clicked.

The trace function draws the cycloid.

The wheel is made up of two rings, a thin ring inside a thick ring, and three spokes. To draw the wheel, we translate our coordinate system to the center of the circle, rotate it by the angle the wheel has rotated through, and then draw the rings and the spokes.

wheel : Float -> Float -> Svg msg
wheel radius rotn =
    let
        cX =
            radius * rotn

        cY =
            svgheight - radius

        tfmStr =
            "translate("
                ++ fromFloat cX
                ++ ","
                ++ fromFloat cY
                ++ ")"
                ++ "rotate("
                ++ (rotn * 180 / pi |> fromFloat)
                ++ ")"
    in
    g
        [ transform tfmStr ]
        [ ring radius "#536600" 4
        , spoke radius "#cc6008" 0
        , spoke radius "#562177" 120
        , spoke radius "#c10764" 240
        , ring radius "#c0c566" 1
        ]

A curious aspect of doing graphics with Elm is that SVG and not canvas is used most of the time. There is a third-party package for doing graphics with canvas and there is also webgl. But we shall not talk about those things now. The point is that drawing on a canvas is a side-effect. There is no DOM property of canvas that changes when drawing is done on it. On the other hand any drawing on an SVG involves the creation of a new SVG node, or the modification of an attribute of an SVG node, or both. Consequently, it is easier to write the view function as a pure function that takes in a new model and produces a new drawing with SVG than with canvas.

Here is the entire code.