Hypocycloids

The applet above generates hypocycloids. A hypocycloid is the path traced by a point on a wheel rolling inside a circle. In the applet you can change the radius of the wheel and also the radius of the point that traces the path. In the post on cycloids both these were fixed.

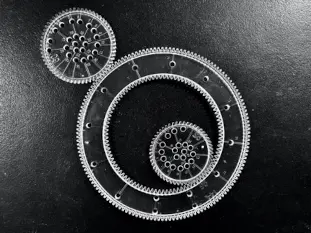
Hypocycloids are some of the patterns that can be drawn by a toy called the Spirograph(shown above) invented by the British engineer Denys Fisher. Here is a page containing a video about him. The Spirograph can also draw epicycloids - these are paths traced by a point on a wheel rolling outside a circle.

Let us try to obtain an equation for the hypocycloid. In the figure above, $r$ is the radius of the track and $r_d$ the radius of the disc rolling inside it. $r_C$ is the distance of the center of the disc from the center of the track and $r_h$ the distance of the point p, which traces the hypocycloid, from the center of the disc.

Consider the motion of the point p from a reference frame attached to the center of the disc(let us call it the disc frame). For a rotation of angle $\theta$ in this frame, the coordinates of the point p are

x = r_h\cos\theta \\ y = r_h\sin\theta

To obtain the equation of the hypocycloid, we need to transform these coordinates to a reference frame attached to the circular track(let us call it the track frame). Let us place the origin of the track frame at the center of the track. If $(X_C, Y_C)$ are the coordinates of the center of the disc in the track frame, the transformed coordinates of the point p are

X = X_C + x = X_C + r_h\cos\theta \\ Y = Y_C + y = Y_C + r_h\sin\theta

In the disc frame, a point on the edge of the disc moves a distance $r_d\theta$ along the circumference when it rotates through the angle $\theta$ . This is the same distance that the disc has rolled along the circular track. Therefore, a line connecting the center of the track with the point of contact of the disc with the track will rotate through an angle $\alpha$ given by

r\alpha = r_d\theta

\alpha = \frac{r_d}{r}\theta

There is one more thing. Notice that when the disc rotates clockwise, the disc moves anti-clockwise along the track. Therefore,

\alpha = -\frac{r_d}{r}\theta

We can then obtain the coordinates for the center of the disc.

X_C = r_C\cos\alpha = r_C\cos\frac{r_d\theta}{r}

Y_C = r_C\sin\alpha = -r_C\sin\frac{r_d\theta}{r}

Then the equation of the hypocycloid is

X = r_C\cos\frac{r_d\theta}{r} + r_h\cos\theta

Y = -r_C\sin\frac{r_d\theta}{r} + r_h\sin\theta

To find out the range of $\theta$ that will give a complete trace of the hypocycloid we have to find out the angle beyond which the path repeats. That is, we have to find out the period in $\theta$ in the above equation. Let $\phi$ be that period. Then

\cos(\frac{r_d}{r}(\theta + \phi)) = \cos(\frac{r_d\theta}{r})

\cos(\theta + \phi) = \cos\theta

where we have demanded each term in $X$ to be periodic with the period $\phi$ . This clearly means that

\frac{r_d\phi}{r} = 2\pi n

\phi = 2\pi m

\frac{r_d}{r} = \frac{n}{m}

where m, n are integers with $m > n$ since $r > r_d$ . So we find out the two smallest integers that are in the ratio $r_d/r$ . The larger of the two gives the number of multiples of $2\pi$ we have to let $\theta$ range through.

As in the cycloid post, I use Elm. Please look at that post for a brief introduction to Elm. The user interface of the applet allows a variety of inputs and changes in state. Surely, there are quite a few ways to model the application to handle these changes in state. What I describe below is just one way.

First, I define some custom types. It is customary to give the same name to the variant as the type when there is only one variant.

type Center
    = Center Float Float

type Radius
    = Radius Float

type Rotn
    = Rotn Float

type Hidden
    = Hidden Bool

type Disc
    = Disc Center Radius Rotn Hidden

type Color
    = Hex String

type Pen
    = Pen Radius Color

The Center type represents the x and y coordinates of the center of the disc. The Radius type is used to specify the radius of the disc as well as the radius of the point(the pen) that traces the hypocycloid. Rotn specifies the rotation of the disc. The input of type color produces its value as a hexadecimal string representing the RGB values of the chosen color. The Color type represents that hexadecimal string. The Disc type represents the rolling disc with a certain center, radius, and angle of rotation that can be hidden or not. The Pen type represents the tracing point at a certain radius from the center of the disc tracing the hypocycloid with a certain color.

discRadius, discRotn, penColor etc are simple functions used to return the data encapsulated by the Disc and Pen types. Notice that they use destructuring to do their work.

discRadius : Disc -> Float
discRadius (Disc _ (Radius r) _ _) =
    r


discRotn : Disc -> Float
discRotn (Disc _ _ (Rotn theta) _) =
    theta


discHidden : Disc -> Bool
discHidden (Disc _ _ _ (Hidden h)) =
    h


penRadius : Pen -> Float
penRadius (Pen (Radius r) _) =
    r


penColor : Pen -> String
penColor (Pen _ (Hex clr)) =
    clr

Here is the Model:

type alias Model =
    { trackR : Float
    , sliders : SliderVals
    , disc : Disc
    , pen : Pen
    , turns : Int
    , path : String
    , svgPaths : Array (Svg Msg)
    , running : Bool
    }

type alias SliderVals =
    { disc : Int
    , pen : Int
    }

trackR is the radius of the track inside which the disc rolls. This is fixed by the width of the container element that holds the SVG and the user interface elements. turns is the number of turns the disc has to go through to produce a complete path. path is the d attribute of the current SVG path. svgPaths is an array of previously drawn hypocycloids. running is true when a hypocycloid is being drawn. sliders stores the values of the range inputs for the disc and pen radii. Both these values are considered to be fractions of the track radius when the actual radii are calculated.

As we have seen in the cycloid post the events fired by the user interface elements are handled by the variants of the Msg type:

type Msg
    = AppHolder (Result Error Element)
    | DiscR String
    | PenR String
    | HexColor String
    | HideDisc Bool
    | Clear
    | Resized
    | Draw
    | NextFrame Float
    | Download

The DiscR and PenR messages handle changes in the disc and pen radii. Since the pen radius is a fraction of the disc radius a change in the disc radius also causes a change in the pen radius.

update : Msg -> Model -> ( Model, Cmd Msg )
update msg model =
    ...
    DiscR val ->
        let
            discVal =
                Maybe.withDefault 1 (toInt val)

            turns =
                10 // gcd discVal 10

            sliders =
                model.sliders

            newSliders =
                { sliders | disc = discVal }

            discR =
                0.1 * (discVal |> toFloat) * model.trackR

            penR =
                0.1 * (model.sliders.pen |> toFloat) * discR

            cx =
                model.trackR - discR

            newDisc =
                model.disc |> updateDisc (CenterChange (Center cx 0)) |> updateDisc (RadiusChange (Radius discR))

            newPen =
                model.pen |> updatePen (RadiusChange (Radius penR))
        in
        ( { model | sliders = newSliders, disc = newDisc, pen = newPen, turns = turns }, Cmd.none )

    PenR val ->
        let
            penVal =
                Maybe.withDefault 1 (toInt val)

            sliders =
                model.sliders

            newSliders =
                { sliders | pen = penVal }

            penR =
                0.1 * (penVal |> toFloat) * discRadius model.disc

            newPen =
                model.pen |> updatePen (RadiusChange (Radius penR))
        in
        ( { model | sliders = newSliders, pen = newPen }, Cmd.none )

I have defined a type to handle the few ways a Disc and Pen can change.

type Param
    = CenterChange Center
    | RadiusChange Radius
    | RotnChange Rotn
    | HideChange Hidden
    | ColorChange Color

The updateDisc and updatePen functions take a parameter of type Param and return a new Disc or Pen.

updateDisc : Param -> Disc -> Disc
updateDisc p (Disc (Center cx cy) (Radius r) (Rotn theta) (Hidden h)) =
    case p of
        CenterChange (Center x y) ->
            Disc (Center x y) (Radius r) (Rotn theta) (Hidden h)

        RadiusChange (Radius newR) ->
            Disc (Center cx cy) (Radius newR) (Rotn theta) (Hidden h)

        RotnChange (Rotn newTheta) ->
            Disc (Center cx cy) (Radius r) (Rotn newTheta) (Hidden h)

        HideChange (Hidden newH) ->
            Disc (Center cx cy) (Radius r) (Rotn theta) (Hidden newH)

        _ ->
            Disc (Center cx cy) (Radius r) (Rotn theta) (Hidden h)


updatePen : Param -> Pen -> Pen
updatePen p (Pen (Radius r) (Hex clr)) =
    case p of
        RadiusChange (Radius newR) ->
            Pen (Radius newR) (Hex clr)

        ColorChange (Hex newClr) ->
            Pen (Radius r) (Hex newClr)

        _ ->
            Pen (Radius r) (Hex clr)

Notice how we use the partial application feature with respect to these functions in the update function.

The AppHolder, HexColor, HideDisc, Clear, and Resized messages are more or less straightforward or have been discussed in the post on cycloids. The Download message is for downloading the hypocycloids drawn as an svg file. Elm makes it rather easy to download an image or text file from a web page with the elm/file package.

The Draw button is handled by the Draw message. Here we set the center of the disc to its starting position, set its angle of rotation to 0, initialize the path's d attribute and set running to true. This starts a subscription to requestAnimationFrame messages which arrive at the update function in the form of NextFrame messages. It is there we increment the angle of rotation, and use the formulas above to calculate the new center of the disc and a new point on the hypocycloid. When the disc has rotated through the required number of turns we set running to false and add the current hypocycloid path to the array of previous paths, ready for a fresh hypocycloid.

update : Msg -> Model -> ( Model, Cmd Msg )
update msg model =
    ...
Draw ->
    let
        rC =
            model.trackR - discRadius model.disc

        newDisc =
            model.disc
                |> updateDisc (CenterChange (Center rC 0))
                |> updateDisc (RotnChange (Rotn 0))

        x =
            rC + penRadius model.pen

        newPath =
            "M " ++ fromFloat x ++ ", 0"
    in
    ( { model | disc = newDisc, path = newPath, running = True }, Cmd.none )

NextFrame _ ->
    if discRotn model.disc <= (toFloat model.turns * 2 * pi) then
        let
            trackR =
                model.trackR

            discR =
                discRadius model.disc

            newRotn =
                discRotn model.disc + angleInc

            cRotn =
                0.1 * toFloat model.sliders.disc * newRotn

            rC =
                trackR - discR

            cx =
                rC * cos cRotn

            cy =
                -rC * sin cRotn

            ( x, y ) =
                pathPoint (Center cx cy) (Rotn newRotn) (penRadius model.pen)

            newDisc =
                model.disc
                    |> updateDisc (CenterChange (Center cx cy))
                    |> updateDisc (RotnChange (Rotn newRotn))

            newPathStr =
                model.path ++ " L " ++ fromFloat x ++ "," ++ fromFloat y
        in
        ( { model | disc = newDisc, path = newPathStr }, Cmd.none )

    else
        let
            (Pen _ c) =
                model.pen

            newPaths =
                Array.push (svgpath model.path c) model.svgPaths
        in
        ( { model | path = "", svgPaths = newPaths, running = False }, Cmd.none )

The view function is more involved than it was in the cycloids post because of the user interface elements.

view : Model -> Html Msg
view model =
    let
        discSldrVal =
            fromInt model.sliders.disc

        penSldrVal =
            fromInt model.sliders.pen

        colorVal =
            penColor model.pen

        colorDsbld =
            model.running

        sldrDsbld =
            model.running || discHidden model.disc

        dwnLoadDsbld =
            model.running || Array.isEmpty model.svgPathStrs
    in
    div [ HA.class "vert_flex", HA.class "app_content" ]
        [ div [ HA.class "svg_content" ]
            [ makeDrawing model ]
        , div [ HA.id "controls", HA.class "vert_flex" ]
            [ label [ HA.class "horiz_flex", HA.class "lbl_in" ]
                [ input [ HA.type_ "checkbox", onCheck HideDisc, HA.checked (discHidden model.disc) ] []
                , Html.text "Hide Disc"
                ]
            , div [ HA.class "horiz_flex" ]
                [ lblledInput "range" "Disc size" DiscR discSldrVal sldrDsbld
                , lblledInput "color" "Color" HexColor colorVal colorDsbld
                , lblledInput "range" "Pen radius" PenR penSldrVal sldrDsbld
                ]
            , div [ HA.class "horiz_flex" ]
                [ button [ onClick Draw, HA.disabled model.running ] [ Html.text "Draw" ]
                , button [ onClick Clear, HA.disabled model.running ] [ Html.text "Clear" ]
                , button [ onClick Download, HA.disabled dwnLoadDsbld ] [ Html.text "Download image" ]
                ]
            ]
        ]

makeDrawing and the subsidiary discAndPaths do the actual drawing.

makeDrawing : Model -> Svg Msg
makeDrawing model =
    let
        rStr =
            fromFloat model.trackR

        w =
            fromFloat (model.trackR * 2)

        moveToCntr =
            "translate("
                ++ rStr
                ++ ","
                ++ rStr
                ++ ")"
    in
    svg
        [ SA.width w
        , SA.height w
        ]
        [ g [ transform moveToCntr ]
            (discAndPaths model)
        ]


discAndPaths : Model -> List (Svg Msg)
discAndPaths model =
    let
        (Pen r c) =
            model.pen

        allPaths =
            if model.path /= "" then
                model.svgPaths |> Array.push (svgpath model.path c)

            else
                model.svgPaths
    in
    if discHidden model.disc then
        allPaths |> Array.toList

    else
        track model.trackR
            :: (allPaths
                    |> Array.push (discDraw model.disc r)
                    |> Array.toList
               )

The other subsidiary functions are more or less similar to the ones in the cycloid post. A helper function is used for the sliders and the color input.

lblledInput : String -> String -> (String -> Msg) -> String -> Bool -> Html Msg
lblledInput typ lbl msgr val dsbl =
    let
        inputAttrbs =
            if typ == "range" then
                [ HA.type_ typ, HA.min "1", HA.max "9", value val, onInput msgr, HA.disabled dsbl ]

            else
                [ HA.type_ typ, value val, onInput msgr, HA.disabled dsbl ]
    in
    div [ HA.class "vert_flex", HA.class "lbl_in" ]
        [ label [] [ Html.text lbl ]
        , input inputAttrbs []
        ]

Here, (String -> Msg) is a function that takes a string and produces a Msg variant. That is, the tags of the variants of the Msg type act as constructor functions of the variants.

Here is the entire code.